获取N个数据中最大的k个数

写代码实现，对长度为N (N非常大,不能一次放入内存)的乱序整数集合，获取它的Top K（可以放到内存）个元素。

思路

在内存中维护(K)个元素的小顶堆，遍历一遍N，每个元素判断是否大于堆顶元素，大于则替换堆顶，向下调整，保持小顶堆。重复上述步骤，最后堆中留下的就是top N。

代码

相关知识

小顶堆

小顶堆是一种经过排序的完全二叉树，其中任一根节点的数据值均不大于其左子节点和右子节点的值。则其根(堆顶)存储的就是整个堆中最小的值。

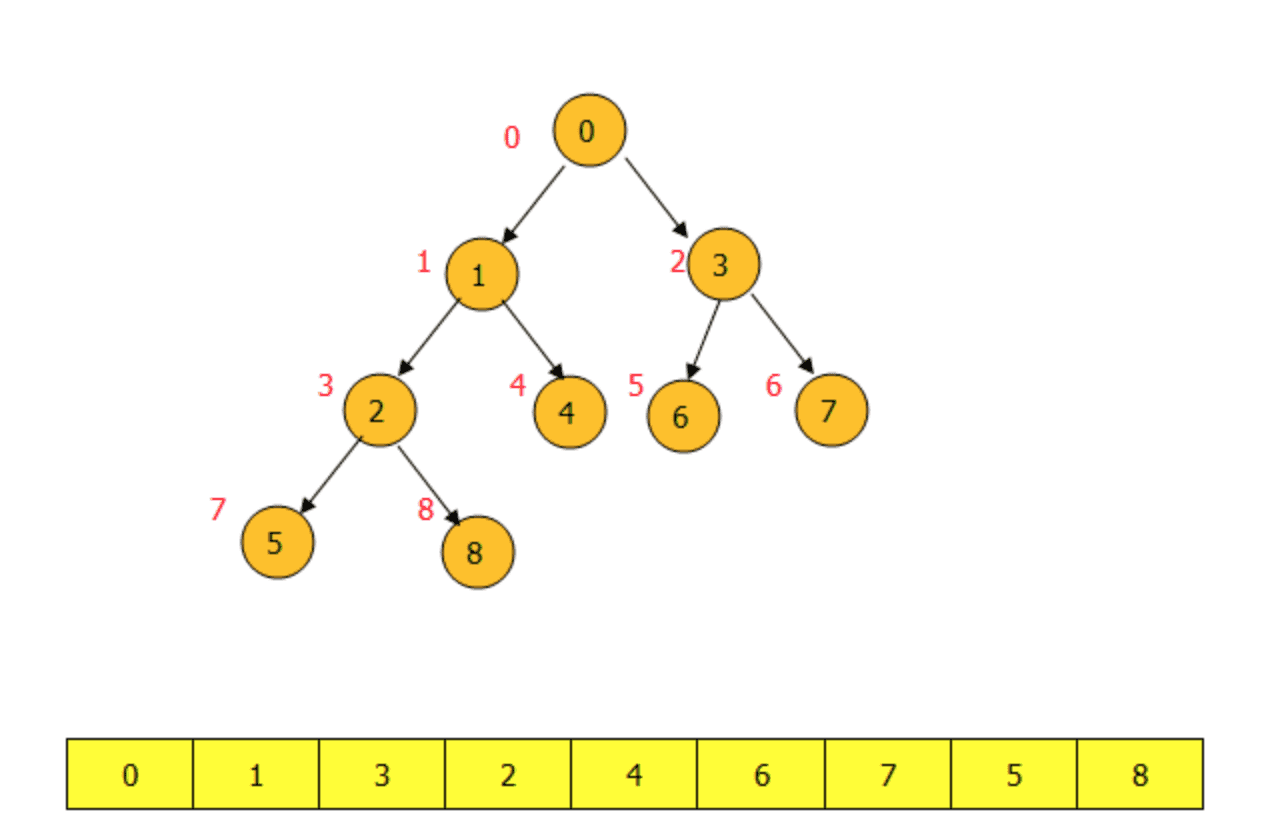
小顶堆建堆代码

public class LitHeapKest {

    static int []a = new int[]{9,8,7,6,5,4,3,2,1,0};
    public static void main(String[] args) {
        for (int i = 1;i<a.length;i++){
            addj(i,a[i]);
        }
        print();
    }

    //n 加入的数，k 加入n的index
    private static void addj(int k,int n){

        int len = a.length ;

        while(k<len && (k-1) >= 0){
            //查看父节点
            int parent = (k-1)/2;
            //父节点小 跳过处理
            if( a[parent] <= n ){
                break;
            }

            //父节点大  和父节点交换
            //（当前k位置放入父节点数据，n作为父节点数据继续向上比较）
            a[k] = a[parent];
            k = parent;

        }
        a[k] = n ;
    }

    private  static void print(){
        for (int i = 0;i<a.length;i++){
            System.out.print(a[i]+" ");
        }
    }
}

替换堆顶元素后向下调整为小顶堆

public class LitHeapKest {

    static int []a = new int[]{9,8,7,6,4,3,2,1,0};
    public static void main(String[] args) {
        //建堆
        for (int i = 1;i<a.length;i++){
            addj(i,a[i]);
        }
        print();
        //替换堆顶后重新调整
        swap(5);
        System.out.println();
        print();
    }

    private static void swap(int n) {
        if (a[0] < n) {
            a[0] = n;//这时候可能破坏了小顶堆
        }

        addjdown();
    }

    //堆顶改变之后向下调整
    private static void addjdown(){
        //替换的堆顶位置
        int pos = 0 ;
        int len = a.length;
        //堆顶的左子结点
        int sub = pos*2+1;

        //存在此子节点
        while (sub < len){
            //找出直接子节点的最的
            if(sub+1 <len && a[sub] > a[sub+1] ){
                sub ++ ;
            }

            //小于最小 不处理
            if(a[pos] < a[sub]){
                break;
            }

            //大于最小 交换后
            int tmp = a[pos];
            a[pos] = a[sub];
            a[sub] = tmp;

            //交换后的子节点继续向下调整
            pos = sub;
            sub = pos*2+1;
        }
    }

    //n 加入的数，k 加入n的index
    private static void addj(int k,int n){

        int len = a.length ;

        while(k<len && (k-1) >= 0){
            //查看父节点
            int parent = (k-1)/2;
            //父节点小 跳过处理
            if( a[parent] <= n ){
                break;
            }

            //父节点大  和父节点交换
            //（当前k位置放入父节点数据，n作为父节点数据继续向上比较）
            a[k] = a[parent];
            k = parent;

        }
        a[k] = n ;
    }

    private  static void print(){
        for (int i = 0;i<a.length;i++){
            System.out.print(a[i]+" ");
        }
    }
}

代码实现

public class TopKFromN {

    int k = 5; //topK
    int m = 13;  //一次取进内存的最大量
    int n = 102; //n

    int[] pool = new int[n];

    public TopKFromN() {
        initPool();
    }

    //mock磁盘中的n
    private void initPool() {

        for (int i = 0; i < n; i++) {
            pool[i] = RandomUtils.nextInt(0, n + 1);
        }
    }

    //取m个进内存
    private int[] getPerBatch(int batch) {

        int startPos = (batch - 1) * m;
        int endPos = (batch) * m; //不包含
        if (endPos > n) {
            endPos = n;
        }
        int length = endPos - startPos;
        int b[] = new int[length];

        System.arraycopy(pool, startPos, b, 0, length);
        return b;
    }

    private int[] getTopK() {

        int topK[] = new int[k];
        boolean initHeap = false;

        //内存批次
        int batchSize = (n - 1) / m + 1;

        for (int x = 1; x <= batchSize; x++) {
            //一次性装进内存
            int startPos = 0 ;
            int b[] = getPerBatch(x);

            for (int pos = 0 ;pos<b.length;pos++){
                if(!initHeap){
                    //add
                    add(topK,b[pos],pos);
                    if(pos == k-1){
                        initHeap = true ;
                    }
                }else {
                    //swap
                    if(topK[0] < b[pos]){
                        swap(topK,b[pos]);
                    }
                }
            }
        }
        return topK;
    }

    //在p位置加入n
    private void add(int []k,final int n,final int p){
        if(p == 0){
            k[0] = n;
            return ;
        }

        int pos = p;
        while(pos>0){
            //找到父节点
            int parent = (pos-1)>>>1;
            if(k[parent] <= n){
                break;
            }
            //父节点大，则和父节点交换
            k[pos] = k[parent];
            //当前位置切换到父节点位置，重复步骤
            pos = parent;
        }
        k[pos] = n;
    }

    private void swap(int []k,int n){
        int pos = 0 ; //替换位置是堆顶
        int sub = pos*2+1; //先找到左子结点

        while (sub < k.length){

            //存在右子节点 ，获取最小值的下标
            if((sub+1)<k.length && k[sub] > k[sub+1]){
                sub ++ ;
            }
            //替换元素小于最小不处理
            if(n < k[sub]){
                break;
            }
            //当前节点和父节点交换
            k[pos] = k[sub];
            //添加的位置切换为最小子节点的位置，向下调整
            pos = sub;
            //重复上述步骤
            sub = pos*2+1;
        }
        //替换掉位置的值
        k[pos] = n;
    }


    public static void main(String[] args) {
        TopKFromN topKFromN = new TopKFromN();

        int[] _k = topKFromN.getTopK();
        printArray(_k);
    }

    private static void printArray(int[] p){
        for (int e:p){
            System.out.print(e +"\t");
        }
        System.out.println();
    }

参考

Java堆结构PriorityQueue完全解析
https://blog.csdn.net/u013309870/article/details/71189189

从简单选择排序到堆排序的深度解析
https://blog.csdn.net/touch_2011/article/details/6767673

海量数据中找出topK
https://blog.csdn.net/suibianshen2012/article/details/52003082

TopK算法
https://blog.csdn.net/dingpiao190/article/details/73604718